4. 5.树¶
4.1. 5.1.基础知识¶
4.1.1. 5.1.1.树的概念¶
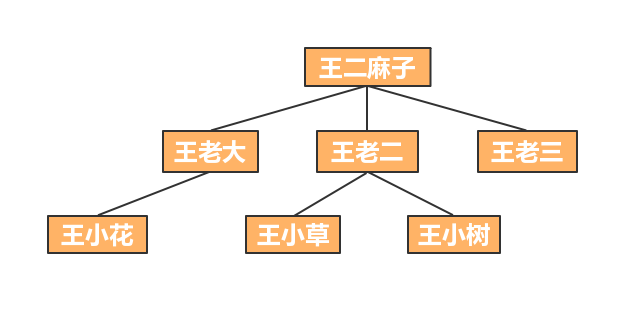
树状图是一种数据结构,它是由n(n>=1)个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点: 每个结点有零个或多个子结点;没有父结点的结点称为根结点;每一个非根结点有且只有一个父结点;除了根结点外,每个子结点可以分为多个不相交的子树。
4.1.1.2. 5.1.1.2.树的术语¶
前面的每个图都是树的示例。树(tree)是一组由边(edge)相连的节点(node),边表示节点间的关系。节点按层(level)组织,层表示节点的层次。最上层的单节点称为根(root)。
树中每个后继层中的节点是前一层中节点的孩子(children)。有孩子的节点称为其孩子的父节点(parent)。如下图所示,节点A是节点B、C、D和E的父节点。因为这些孩子有相同的父节点,所以它们称为兄弟(sibling)。它们也称为节点A的后代(descendant),而节点A是它们的祖先(ancestor)。节点P是节点A的后代,而A是P的祖先。注意,节点P没有孩子。这样的节点称为叶子(leaf)。
不是叶节点的节点–即有孩子的节点–称为内部节点(interior)或非叶节点(nonleaf)。这样的节点也是父节点。
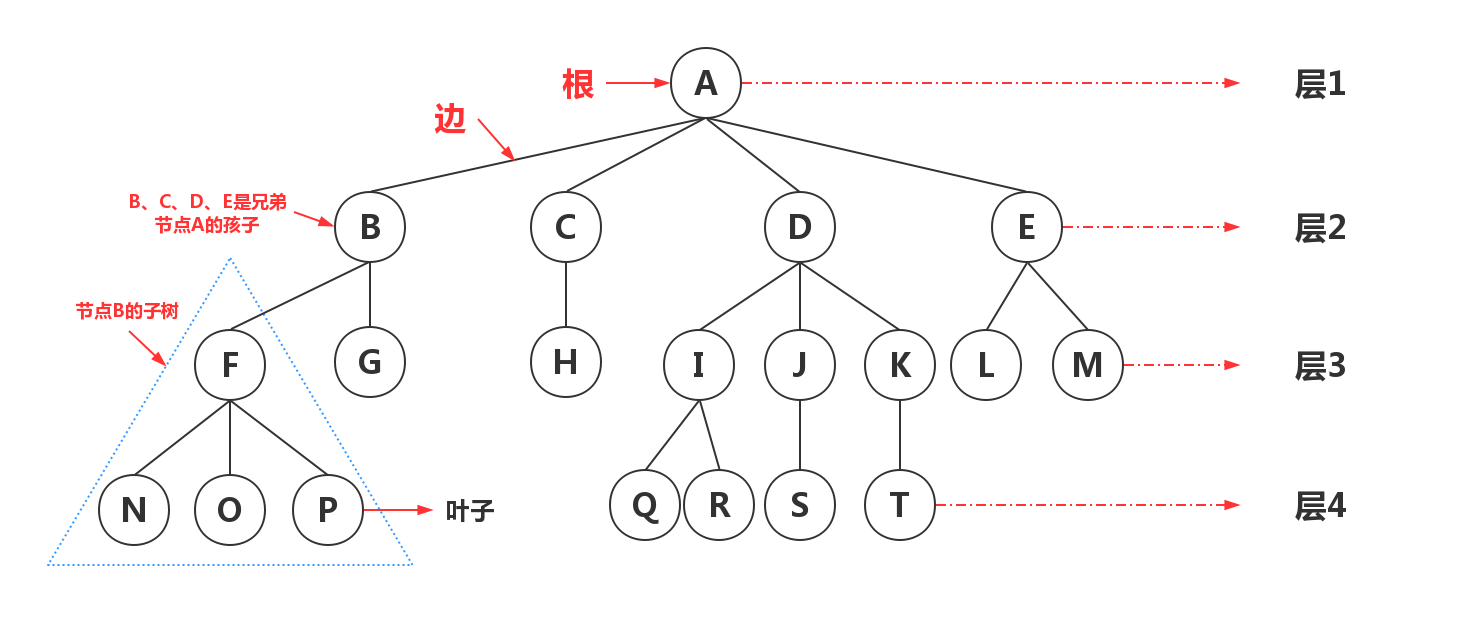
- 根节点或树根(root)
- 树定点的节点称之为根节点,也叫树根
- 节点(Node)
- 树中的每个元素都称为节点
- 子树(SubTree)
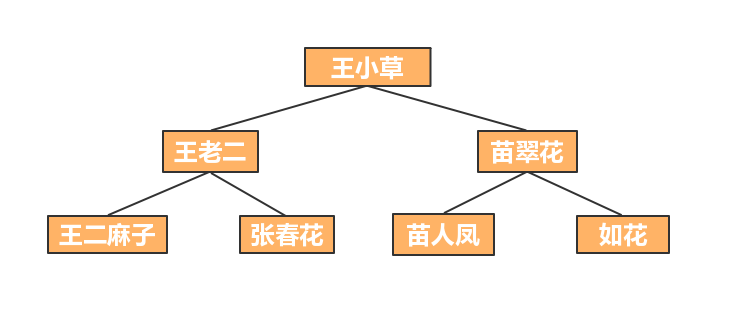
- 除根节点外,其他节点也可以分为多个树的集合,叫做子树,上图中F节点和N、O、P节点共同构成一颗子树,节点B的子树。
- 节点的度
- 一个节点之间含有的子树的个数,称之为节点的度。上图中D节点的度为3,E节点的度为2,Q、R、S节点的度为0
- 叶子节点、叶节点、终端节点
- 度为0的节点叫做叶子节点,也叫叶节点、终端节点。其实就是没有子节点的节点,或者说没有子树的节点。
- 父节点、双亲节点
- 兄弟节点
- 树的度
- 一棵树中最大节点的度称之为树的度,即树中哪个节点的子节点最多,那么这个节点的度也就是树的度。
- 节点的层次
- 从根这一层开始,根算1层,根的子节点算2层,一直到最下面一层
- 树的高度、深度
- 树的深度是从根节点开始、自顶向下逐层累加(根节点的高度是1)助记:深度从上到下 树的高度是从叶节点开始、自底向上逐层累加(叶节点的高度是1)助记:高度由下向上 虽然树的高度和深度一样,但是具体到某个节点上,其高度和深度通常是不一样的。
- 堂兄弟节点
- 节点的祖先
- 节点的子孙
- 森林
- 由m棵不相交的树组成的集合,叫做森林
4.1.1.2.1. 5.1.1.2.1.二叉树¶
二叉树中的每个节点最多有两个孩子。它们称为左孩子(left child)和右孩子(right child)
如图所示:节点B、D、F都是左孩子,二节点C、E、G都是右孩子。该二叉树的根有两颗子树。左子树(left subtree)的根是B,而右子树(right subtree)的根是C。 二叉树中的每颗子树还是二叉树。
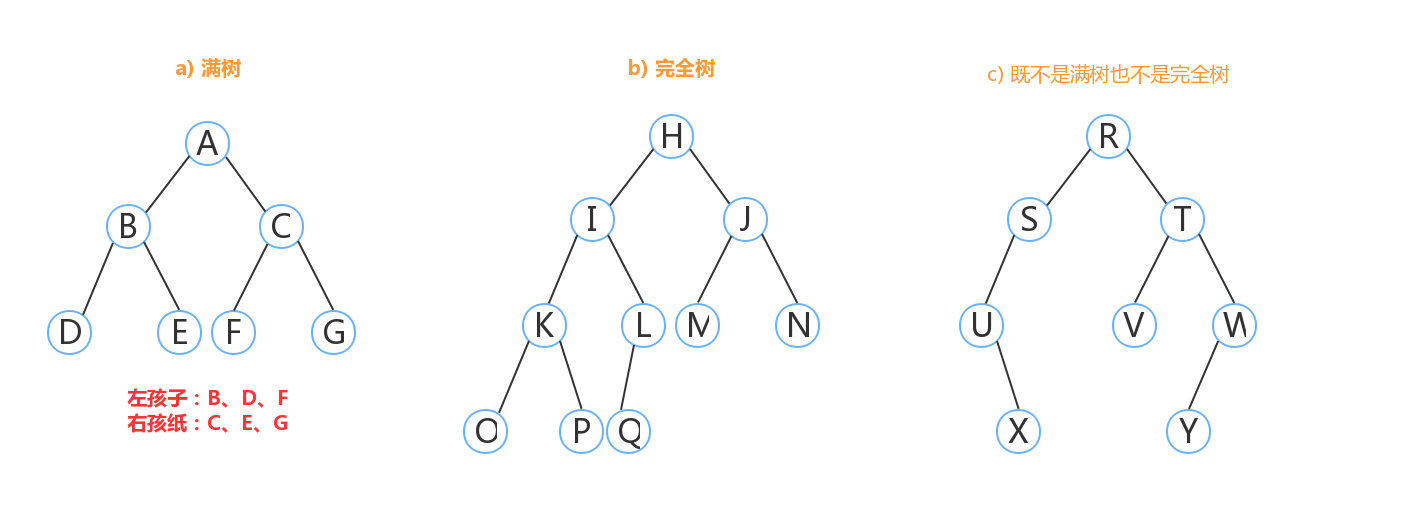
4.1.1.2.2. 5.1.1.2.2.满二叉树和完全二叉树¶
满二叉树:高度为h的二叉树中,若其所有的叶节点都在h层上且每个非叶节点都有两个孩子,则树称为满的。如图a) 既为一颗满二叉树。
完全二叉树:如果二叉树中除最后一层外的所有层都含有最多的节点,最后一层的节点从左至右填充,则树是完全的。如图b)即为一颗完全二叉树
注:满二叉树中的所有叶节点都在同一层中,且每个非叶节点都有两个孩子。完全二叉树中,到倒数第二层都是满的,且最后一层的叶节点从左至右填充。
4.1.1.2.3. 5.1.1.2.3.平衡二叉树¶
若二叉树中每个节点有两颗高度完全相等的子树,则树称为完全平衡树(Completely balanced)。
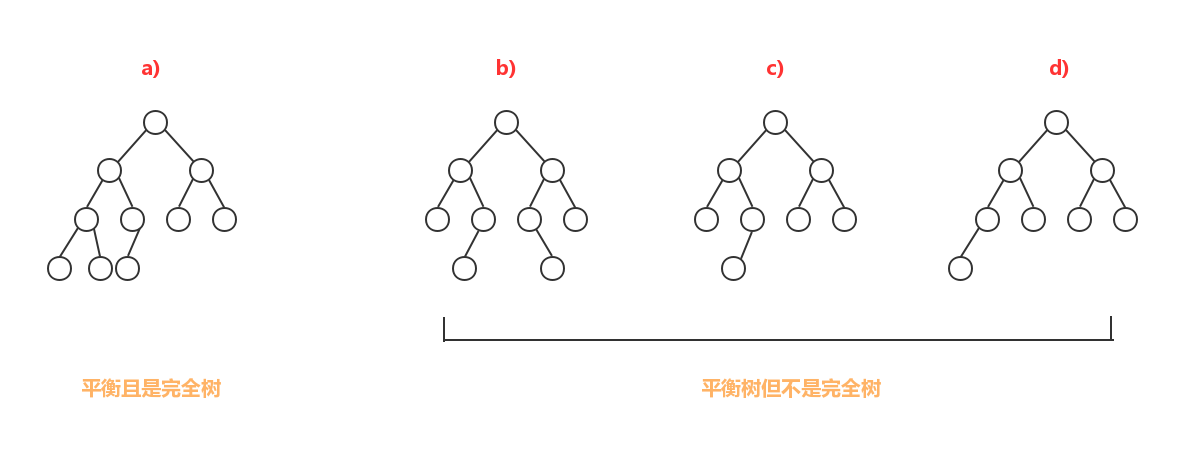
如图所示的满树是完全平衡树。如果树中的每个节点的子树的高度差不大于1,则树称为高度平衡的,或简称为平衡的。
满树或完全树的高度。
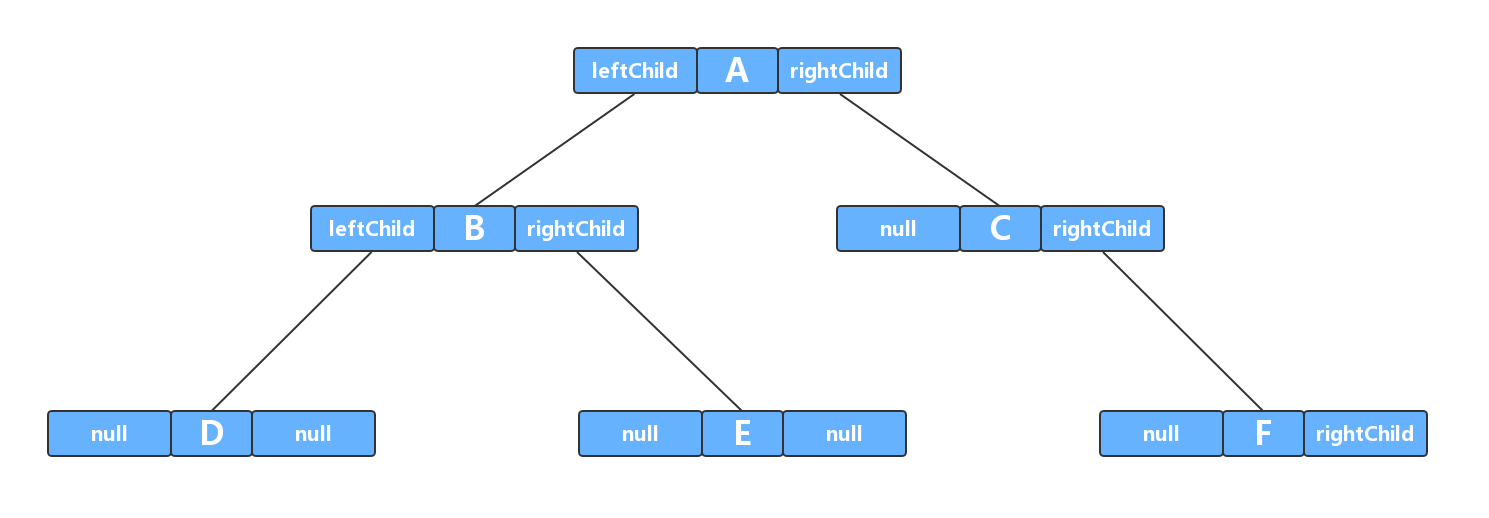
4.1.2. 5.1.2.二叉树中的节点¶
4.1.3. 5.1.3.二叉树实现¶
/**
* All rights Reserved, Designed By https://www.tulingxueyuan.com/
* @Title: BinaryTree.java
* @Package com.tuling.tree
* @Description:
* @author: 小白
* @Date 2019年12月6日 下午10:24:12
* @version V1.0
* @Copyright:
*/
package com.tuling.tree;
/**
* @ClassName BinaryTree
* @Description
* @Author 北京图灵学院
* @Date 2019年12月6日 下午10:24:12
*/
public class BinaryTree {
private TreeNode root = null;
public BinaryTree() {
root = new TreeNode(1, "A");
//自己手动创建一个二叉树
createBinaryTree(root);
}
/**
*
* @Title: createBinaryTree
* @Description:手动创建一个二叉树
* @param: root
* @return: void
* @throws
*/
public void createBinaryTree(TreeNode root) {
TreeNode nodeB = new TreeNode(2, "B");
TreeNode nodeC = new TreeNode(3, "C");
TreeNode nodeD = new TreeNode(4, "D");
TreeNode nodeE = new TreeNode(5, "E");
TreeNode nodeF = new TreeNode(6, "F");
root.leftChild = nodeB;
root.rightChild = nodeC;
root.leftChild.leftChild = nodeD;
root.leftChild.rightChild = nodeE;
root.rightChild.rightChild = nodeF;
}
public TreeNode getRoot() {
return root;
}
public void setRoot(TreeNode root) {
this.root = root;
}
/**
*
* @ClassName TreeNode
* @Description:二叉树的节点数据结构
* @Author 北京图灵学院
* @Date 2019年12月6日 下午10:24:35
*/
private class TreeNode{
private int key;
private String data;
private boolean isVisted;
private TreeNode leftChild;
private TreeNode rightChild;
/**
* @Title: TreeNode
* @Description:
* @param:
* @throws
*/
public TreeNode() {
}
/**
* @Title: TreeNode
* @Description:
* @param: key 层序编码
* @param: data 数据域
* @throws
*/
public TreeNode(int key, String data) {
super();
this.key = key;
this.data = data;
this.leftChild = null;
this.rightChild = null;
}
/**
*
*/
@Override
public String toString() {
return "TreeNode [key=" + key + ", data=" + data + "]";
}
}
}
4.1.4. 5.1.4.二叉树前序遍历代码实现¶
在BinaryTree中增加如下方法:
/**
*
* @Title: preOrder
* @Description:前序遍历:根-->左-->右
* @param:
* @return: void
* @throws
*/
public void preOrder() {
if(root != null) {
root.preOrder();
}else {
System.out.println("树为空!");
}
}
在内部类 TreeNode 中增加如下方法:
/**
* @Title: preOrder
* @Description:前序遍历:根-->左-->右
* @param:
* @return: void
* @throws
*/
public void preOrder() {
//先打印自己,也就是根
System.out.println(this);
//递归遍历左子树
if(this.leftChild!=null) {
this.leftChild.preOrder();
}
//递归遍历右子树
if(this.rightChild!=null) {
this.rightChild.preOrder();
}
}
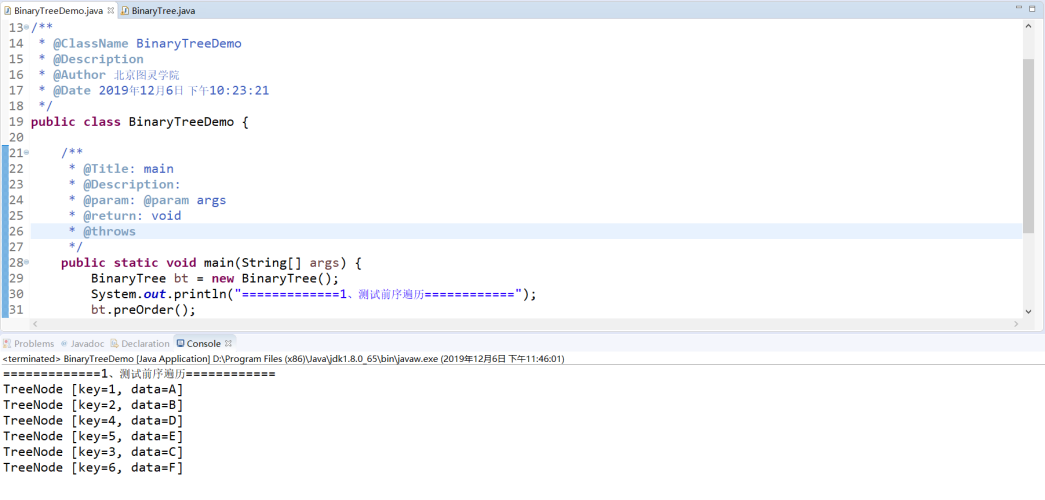
运行效果:
4.1.5. 5.1.5.二叉树中序遍历代码实现¶
在BinaryTree中增加如下方法:
/**
*
* @Title: inFixOrder
* @Description:中序遍历:左-->根-->右
* @param:
* @return: void
* @throws
*/
public void inFixOrder() {
if(root != null) {
root.inFixOrder();
}else {
System.out.println("树为空!");
}
}
在内部类TreeNode中增加如下方法:
/**
* @Title: inFixOrder
* @Description:中序遍历:左-->根-->右
* @param:
* @return: void
* @throws
*/
public void inFixOrder() {
//递归遍历左子树
if(this.leftChild!=null) {
this.leftChild.inFixOrder();
}
//打印自己
System.out.println(this);
//递归遍历右子树
if(this.rightChild!=null) {
this.rightChild.inFixOrder();
}
}
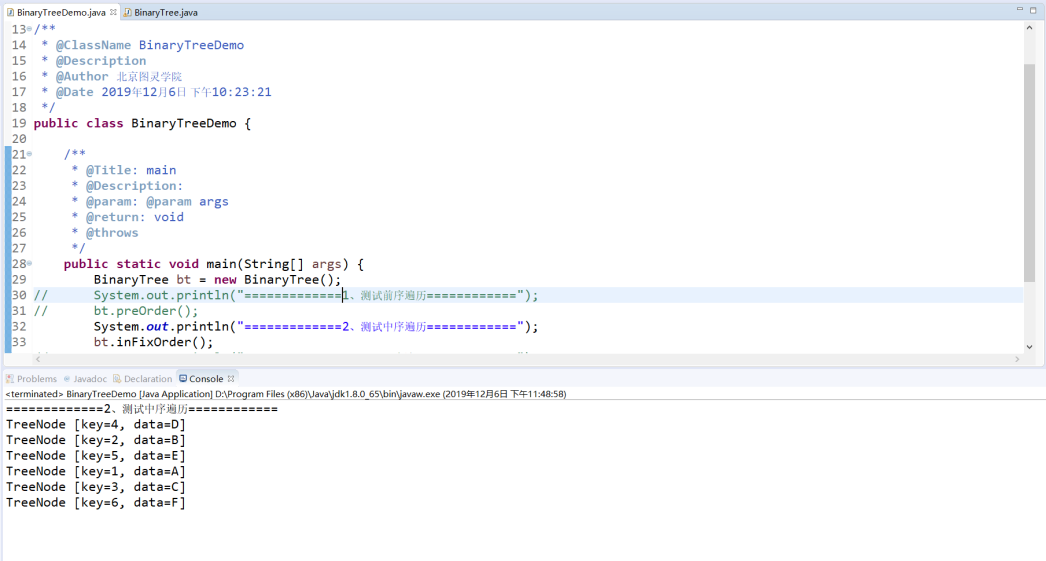
测试效果:
4.1.6. 5.1.6.二叉树后序遍历代码实现¶
在BinaryTree中增加如下方法:
/**
*
* @Title: postOrder
* @Description:后序遍历:左-->右-->根
* @param:
* @return: void
* @throws
*/
public void postOrder() {
if(root!=null) {
root.postOrder();
}else {
System.out.println("树为空!");
}
}
在内部类TreeNode中增加如下方法:
/**
* @Title: postOrder
* @Description:后序遍历:左-->右-->根
* @param:
* @return: void
* @throws
*/
public void postOrder() {
//递归遍历左子树
if(this.leftChild!=null) {
this.leftChild.postOrder();
}
//递归遍历右子树
if(this.rightChild!=null) {
this.rightChild.postOrder();
}
//打印自己
System.out.println(this);
}
测试效果:
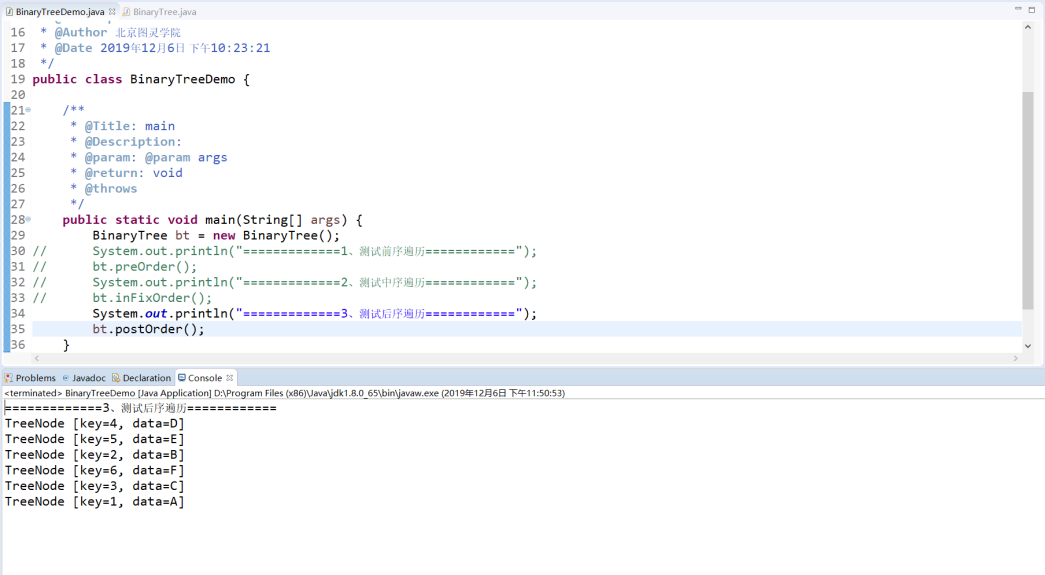
类BinaryTree完整代码如下:
/**
* All rights Reserved, Designed By https://www.tulingxueyuan.com/
* @Title: BinaryTree.java
* @Package com.tuling.tree
* @Description:
* @author: 小白
* @Date 2019年12月6日 下午10:24:12
* @version V1.0
* @Copyright:
*/
package com.tuling.tree;
/**
* @ClassName BinaryTree
* @Description
* @Author 北京图灵学院
* @Date 2019年12月6日 下午10:24:12
*/
public class BinaryTree {
private TreeNode root = null;
public BinaryTree() {
root = new TreeNode(1, "A");
//自己手动创建一个二叉树
createBinaryTree(root);
}
/**
*
* @Title: createBinaryTree
* @Description:手动创建一个二叉树
* @param: root
* @return: void
* @throws
*/
public void createBinaryTree(TreeNode root) {
TreeNode nodeB = new TreeNode(2, "B");
TreeNode nodeC = new TreeNode(3, "C");
TreeNode nodeD = new TreeNode(4, "D");
TreeNode nodeE = new TreeNode(5, "E");
TreeNode nodeF = new TreeNode(6, "F");
root.leftChild = nodeB;
root.rightChild = nodeC;
root.leftChild.leftChild = nodeD;
root.leftChild.rightChild = nodeE;
root.rightChild.rightChild = nodeF;
}
/**
*
* @Title: preOrder
* @Description:前序遍历:根-->左-->右
* @param:
* @return: void
* @throws
*/
public void preOrder() {
if(root != null) {
root.preOrder();
}else {
System.out.println("树为空!");
}
}
/**
*
* @Title: inFixOrder
* @Description:中序遍历:左-->根-->右
* @param:
* @return: void
* @throws
*/
public void inFixOrder() {
if(root != null) {
root.inFixOrder();
}else {
System.out.println("树为空!");
}
}
/**
*
* @Title: postOrder
* @Description:后序遍历:左-->右-->根
* @param:
* @return: void
* @throws
*/
public void postOrder() {
if(root!=null) {
root.postOrder();
}else {
System.out.println("树为空!");
}
}
public TreeNode getRoot() {
return root;
}
public void setRoot(TreeNode root) {
this.root = root;
}
/**
*
* @ClassName TreeNode
* @Description:二叉树的节点数据结构
* @Author 北京图灵学院
* @Date 2019年12月6日 下午10:24:35
*/
private class TreeNode{
private int key;
private String data;
private boolean isVisted;
private TreeNode leftChild;
private TreeNode rightChild;
/**
* @Title: TreeNode
* @Description:
* @param:
* @throws
*/
public TreeNode() {
}
/**
* @Title: postOrder
* @Description:后序遍历:左-->右-->根
* @param:
* @return: void
* @throws
*/
public void postOrder() {
//递归遍历左子树
if(this.leftChild!=null) {
this.leftChild.postOrder();
}
//递归遍历右子树
if(this.rightChild!=null) {
this.rightChild.postOrder();
}
//打印自己
System.out.println(this);
}
/**
* @Title: inFixOrder
* @Description:中序遍历:左-->根-->右
* @param:
* @return: void
* @throws
*/
public void inFixOrder() {
//递归遍历左子树
if(this.leftChild!=null) {
this.leftChild.inFixOrder();
}
//打印自己
System.out.println(this);
//递归遍历右子树
if(this.rightChild!=null) {
this.rightChild.inFixOrder();
}
}
/**
* @Title: preOrder
* @Description:前序遍历:根-->左-->右
* @param:
* @return: void
* @throws
*/
public void preOrder() {
//先打印自己,也就是根
System.out.println(this);
//递归遍历左子树
if(this.leftChild!=null) {
this.leftChild.preOrder();
}
//递归遍历右子树
if(this.rightChild!=null) {
this.rightChild.preOrder();
}
}
/**
* @Title: TreeNode
* @Description:
* @param: key 层序编码
* @param: data 数据域
* @throws
*/
public TreeNode(int key, String data) {
super();
this.key = key;
this.data = data;
this.leftChild = null;
this.rightChild = null;
}
/**
*
*/
@Override
public String toString() {
return "TreeNode [key=" + key + ", data=" + data + "]";
}
}
}
4.2. 5.2.二叉查找树的实现¶
4.2.1. 5.2.1.入门知识¶
二叉查找树(Binary Search Tree),(又:二叉搜索树,二叉排序树)它或者是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。
4.2.2. 5.2.2.添加¶
4.2.2.1. 5.2.2.1.递归实现¶
在BinarySearchTree.java 中添加如下代码:
/**
*
* @Title: add
* @Description:二叉查找树添加的方法
* @param: data
* @return: void
* @throws
*/
public void add(Comparable data) {
if(root == null) {
root = new Node(data);
}else {
root.add(data);
}
}
在内部类 Node.java 中添加如下代码:
/**
* @Title: add
* @Description:添加方法
* 实现:调用 Comparable 接口的 compareTo 方法,比较对象大小
* 1、如果当前对象小于指定对象,返回负整数
* 2、如果当前对象等于指定对象,返回0
* 3、如果当前对象大于指定对象,返回正整数
*
* 如果返回正整数,进左子树
* 如果返回负整数或0,进右子树
* @param: data
* @return: void
* @throws
*/
public void add(Comparable data) {
if(this.data.compareTo(data) > 0) {
if(this.left==null) {
this.left = new Node(data);
}else {
this.left.add(data);
}
}else if(this.data.compareTo(data) <= 0) {
if(this.right == null) {
this.right = new Node(data);
}else {
this.right.add(data);
}
}
}
4.2.3. 5.2.3.遍历¶
在BinarySearchTree.java类中添加如下代码:
/**
*
* @Title: inFixOrder
* @Description:中序遍历
* @param:
* @return: void
* @throwss
*/
public void inFixOrder() {
if(root == null) {
System.out.println("树为空!");
}else {
root.inFixOrder();
}
}
在内部类Node.java中添加如下代码:
/**
* @Title: inFixOrder
* @Description:中序遍历
* @param:
* @return: void
* @throws
*/
public void inFixOrder() {
//先遍历左子树
if(this.left!=null) {
this.left.inFixOrder();
}
//打印数据
System.out.println(this);
//遍历右子树
if(this.right!=null) {
this.right.inFixOrder();
}
}
测试代码:
/**
* All rights Reserved, Designed By https://www.tulingxueyuan.com/
* @Title: BinarySearchTreeDemo.java
* @Package com.tuling.tree
* @Description:
* @author: 小白
* @Date 2019年12月7日 上午1:18:33
* @version V1.0
* @Copyright:
*/
package com.tuling.tree;
/**
* @ClassName BinarySearchTreeDemo
* @Description
* @Author 北京图灵学院
* @Date 2019年12月7日 上午1:18:33
*/
public class BinarySearchTreeDemo {
/**
* @Title: main
* @Description:
* @param: @param args
* @return: void
* @throws
*/
public static void main(String[] args) {
BinarySearchTree bst = new BinarySearchTree();
bst.add(25);
bst.add(43);
bst.add(2);
bst.add(765);
bst.add(23);
bst.add(1);
bst.add(76);
bst.inFixOrder();
}
}
运行效果:
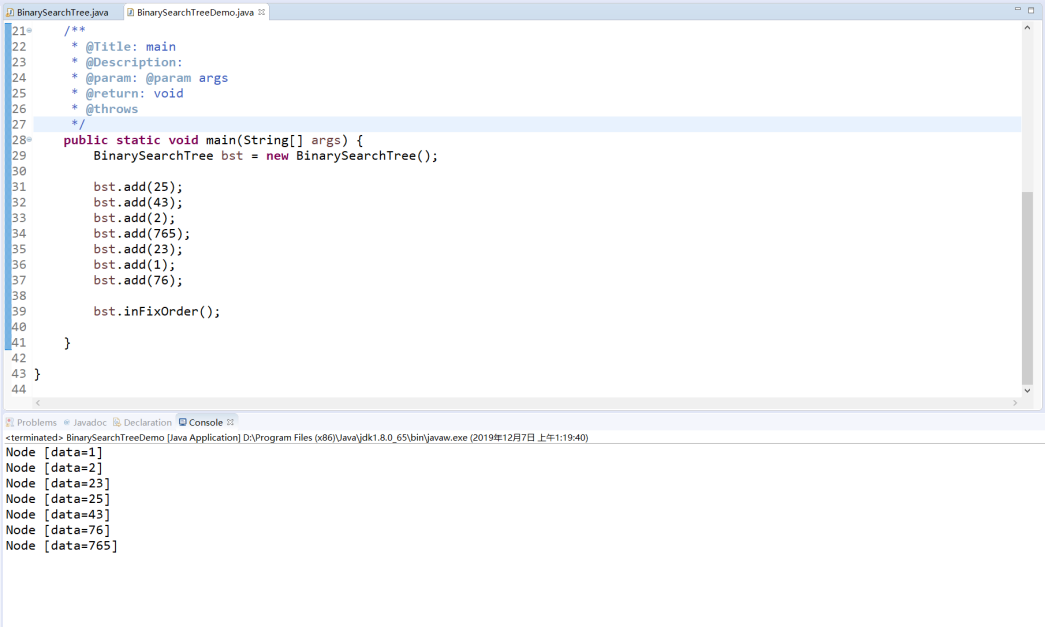
4.2.4. 5.2.4.查找和获取¶
在BinarySearchTree.java类中添加如下代码
/**
*
* @Title: bstSearch
* @Description:查找
* @param: data
* @param:
* @return: Node
* @throws
*/
public Node bstSearch(Comparable data) {
if(root.data.compareTo(data)==0) {
return root;
}else {
return root.bstSearch(data);
}
}
在内部类Node.java中添加如下代码:
/**
* @Title: bstSearch
* @Description:查找
* @param: data
* @param:
* @return: Node
* @throws
*/
public Node bstSearch(Comparable data) {
if(this.data.compareTo(data) == 0) {
return this;
}else if(this.data.compareTo(data)>0) {//如果要查找的对象小于当前对象,向左子树查找。
if(this.left == null) {//如果左子树为空。
return null;
}
//递归向左子树查找。
return this.left.bstSearch(data);
}else if(this.data.compareTo(data) <= 0) {//如果要查找的对象大于或等于当前对象,向右子树查找。
if(this.right == null) {
return null;
}
//递归向右子树查找
return this.right.bstSearch(data);
}
return null;
}
4.2.5. 5.2.5.删除¶
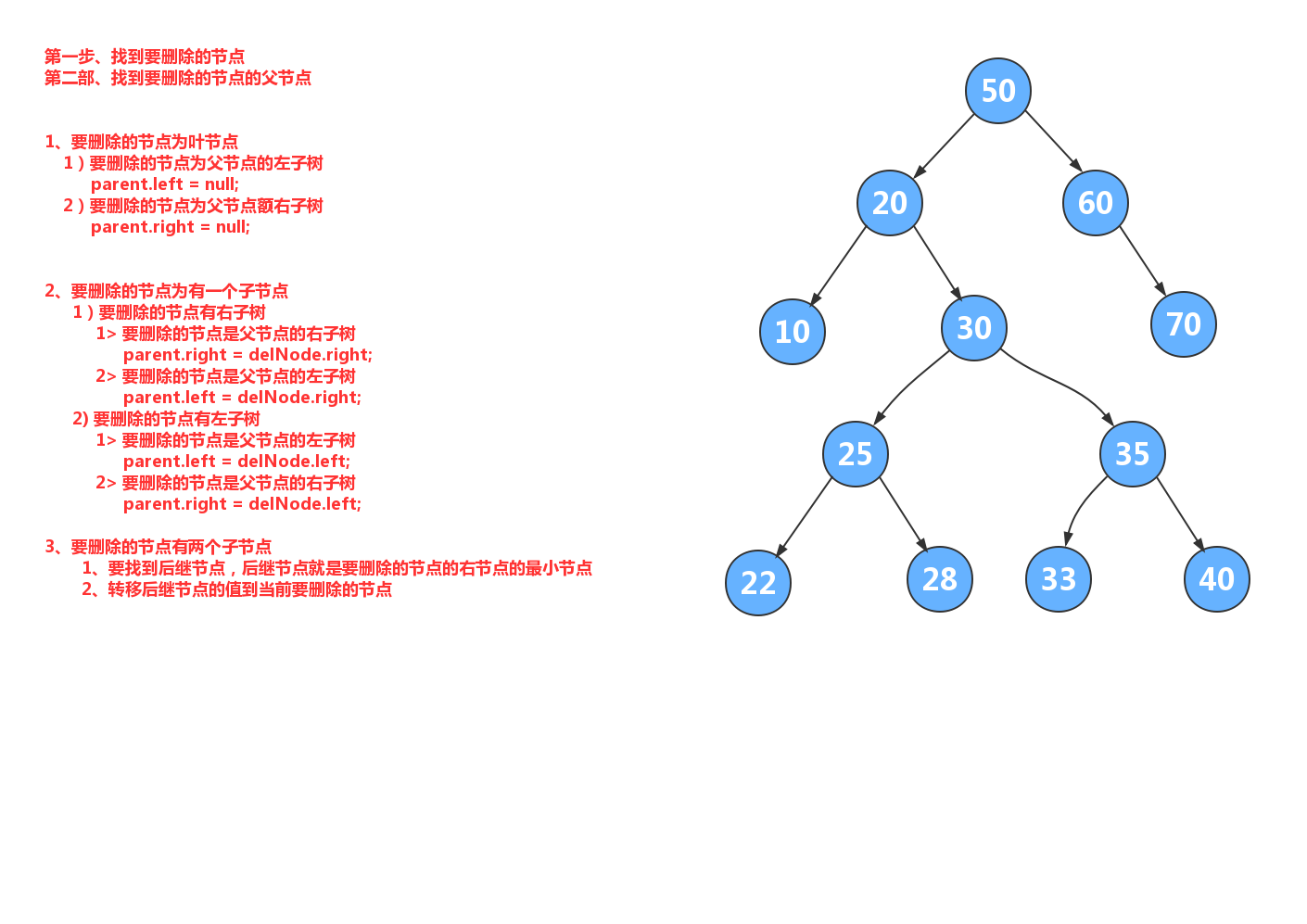
删除功能代码如下:
/**
*
* @Title: del
* @Description:删除
* @param: @param data
* @param: @return
* @return: boolean
* @throws
*/
public void del(Comparable data) {
if(root == null) {
return;
}
//先找到需要删除的节点
Node delNode = bstSearch(data);
//如果没有找到要删除的节点
if(delNode==null) {
return;
}
//找到要删除的节点的父节点
Node parentNode = searchParent(delNode);
//如果要删除的节点是叶节点
if(delNode.left==null && delNode.right==null) {
//判断 delNode 是父节点的左子树还是右子树
if(parentNode.left!=null && parentNode.left.data.equals(delNode.data)) {
parentNode.left = null;
}else if(parentNode.right!=null && parentNode.right.data.equals(delNode.data)) {
parentNode.right = null;
}
}else if(delNode.left!=null && delNode.right!=null) {//要删除的节点有两个子节点
//获取后继节点的数据
Comparable minNodeData = getRightTreeMin(delNode.right);
//转移后继节点的值到当前要删除的节点
delNode.data = minNodeData;
}else {//删除只有一个子树的节点
/*
* 要删除的节点有左子树
*/
if(delNode.left!=null) {
if(parentNode!=null) {//要删除的节点为父节点的左子树
if(parentNode.left!=null && parentNode.left.data.compareTo(delNode.data) == 0) {
parentNode.left = delNode.left;
}else {
//要删除的节点为父节点的右子树
parentNode.right = delNode.left;
}
}else {
//删除的是root
root = delNode.left;
}
}else {//要删除的节点有右子树
if(parentNode!=null) {//要删除的节点为父节点的左子树
if(parentNode.left!=null && parentNode.left.data.compareTo(delNode.data) == 0) {
parentNode.left = delNode.right;
}else {
//要删除的节点为父节点的右子树
parentNode.right = delNode.right;
}
}else {
//删除的是root
root = delNode.right;
}
}
}
}
查找父节点功能代码如下:
/**
* @Title: searchParent
* @Description:查找要删除的节点的父节点
* @param: @param delNode
* @param: @return
* @return: Node
* @throws
*/
private Node searchParent(Node delNode) {
if(root == null) {
return null;
}else {
return this.root.searchParent(delNode);
}
}
内部类Node.java中的代码如下:
/**
* @Title: searchParent
* @Description:递归查找要删除的节点的父节点
* @param: @param delNode
* @param: @return
* @return: Node
* @throws
*/
public Node searchParent(Node delNode) {
//如果当前节点就是要删除节点的父节点
if(this.left!=null && this.left.data.compareTo(delNode.data)==0 ||
this.right!=null && this.right.data.compareTo(delNode.data) == 0) {
return this;
}else {//当前节点不是要删除节点的父节点,需要递归向下遍历查找。
//如果当前对象的左子树不为空,并且要查找的对象小于当前对象,递归向左子树查找。
if(this.left!=null && this.data.compareTo(delNode.data) > 0) {
return this.left.searchParent(delNode);
}else if(this.right!=null && this.data.compareTo(delNode.data) <= 0) {
return this.right.searchParent(delNode);
}else {
//没有找到父节点
return null;
}
}
}
二叉查找树BinarySearchTree.java类完整代码如下:
/**
* All rights Reserved, Designed By https://www.tulingxueyuan.com/
* @Title: BinarySearchTree.java
* @Package com.tuling.tree
* @Description:
* @author: 小白
* @Date 2019年12月7日 上午12:46:43
* @version V1.0
* @Copyright:
*/
package com.tuling.tree;
/**
* @ClassName BinarySearchTree
* @Description
* @Author 北京图灵学院
* @Date 2019年12月7日 上午12:46:43
*/
public class BinarySearchTree {
private Node root;
/**
*
* @Title: add
* @Description:二叉查找树添加的方法
* @param: data
* @return: void
* @throws
*/
public void add(Comparable data) {
if(root == null) {
root = new Node(data);
}else {
root.add(data);
}
}
/**
*
* @Title: inFixOrder
* @Description:中序遍历
* @param:
* @return: void
* @throws
*/
public void inFixOrder() {
if(root == null) {
System.out.println("树为空!");
}else {
root.inFixOrder();
}
}
/**
*
* @Title: bstSearch
* @Description:查找
* @param: data
* @param:
* @return: Node
* @throws
*/
public Node bstSearch(Comparable data) {
if(root == null) {
return null;
}else {
return this.root.bstSearch(data);
}
}
/**
* @Title: searchParent
* @Description:查找要删除的节点的父节点
* @param: @param delNode
* @param: @return
* @return: Node
* @throws
*/
private Node searchParent(Node delNode) {
if(root == null) {
return null;
}else {
return this.root.searchParent(delNode);
}
}
/**
*
* @Title: del
* @Description:删除
* @param: @param data
* @param: @return
* @return: boolean
* @throws
*/
public void del(Comparable data) {
if(root == null) {
return;
}
//先找到需要删除的节点
Node delNode = bstSearch(data);
//如果没有找到要删除的节点
if(delNode==null) {
return;
}
//找到要删除的节点的父节点
Node parentNode = searchParent(delNode);
//如果要删除的节点是叶节点
if(delNode.left==null && delNode.right==null) {
//判断 delNode 是父节点的左子树还是右子树
if(parentNode.left!=null && parentNode.left.data.equals(delNode.data)) {
parentNode.left = null;
}else if(parentNode.right!=null && parentNode.right.data.equals(delNode.data)) {
parentNode.right = null;
}
}else if(delNode.left!=null && delNode.right!=null) {//要删除的节点有两个子节点
//获取后继节点的数据
Comparable minNodeData = getRightTreeMin(delNode.right);
//转移后继节点的值到当前要删除的节点
delNode.data = minNodeData;
}else {//删除只有一个子树的节点
/*
* 要删除的节点有左子树
*/
if(delNode.left!=null) {
if(parentNode!=null) {//要删除的节点为父节点的左子树
if(parentNode.left!=null && parentNode.left.data.compareTo(delNode.data) == 0) {
parentNode.left = delNode.left;
}else {
//要删除的节点为父节点的右子树
parentNode.right = delNode.left;
}
}else {
//删除的是root
root = delNode.left;
}
}else {//要删除的节点有右子树
if(parentNode!=null) {//要删除的节点为父节点的左子树
if(parentNode.left!=null && parentNode.left.data.compareTo(delNode.data) == 0) {
parentNode.left = delNode.right;
}else {
//要删除的节点为父节点的右子树
parentNode.right = delNode.right;
}
}else {
//删除的是root
root = delNode.right;
}
}
}
}
/**
* @Title: getRightTreeMin
* @Description:返回要删除的节点右子树的最小节点
* @param: @param delNode
* @param: @return
* @return: Node
* @throws
*/
private Comparable getRightTreeMin(Node delNode) {
Node tempNode = delNode;
//循环向左查找即可
while(tempNode.left!=null) {
tempNode = tempNode.left;
}
//循环结束,tempNode指向要删除节点右子树的最小节点。
//删除最小节点
del(tempNode.data);
return tempNode.data;
}
/**
*
* @ClassName Node
* @Description:二叉树的节点数据结构
* @Author 北京图灵学院
* @Date 2019年12月7日 上午1:46:33
*/
class Node{
private Comparable data;
private Node left;
private Node right;
/**
* @Title: Node
* @Description:
* @param:
* @throws
*/
public Node() {
super();
}
/**
* @Title: searchParent
* @Description:递归查找要删除的节点的父节点
* @param: @param delNode
* @param: @return
* @return: Node
* @throws
*/
public Node searchParent(Node delNode) {
//如果当前节点就是要删除节点的父节点
if(this.left!=null && this.left.data.compareTo(delNode.data)==0 ||
this.right!=null && this.right.data.compareTo(delNode.data) == 0) {
return this;
}else {//当前节点不是要删除节点的父节点,需要递归向下遍历查找。
//如果当前对象的左子树不为空,并且要查找的对象小于当前对象,递归向左子树查找。
if(this.left!=null && this.data.compareTo(delNode.data) > 0) {
return this.left.searchParent(delNode);
}else if(this.right!=null && this.data.compareTo(delNode.data) <= 0) {
return this.right.searchParent(delNode);
}else {
//没有找到父节点
return null;
}
}
}
/**
* @Title: bstSearch
* @Description:查找
* @param: data
* @param:
* @return: Node
* @throws
*/
public Node bstSearch(Comparable data) {
if(this.data.compareTo(data) == 0) {
return this;
}else if(this.data.compareTo(data)>0) {//如果要查找的对象小于当前对象,向左子树查找。
if(this.left == null) {//如果左子树为空。
return null;
}
//递归向左子树查找。
return this.left.bstSearch(data);
}else if(this.data.compareTo(data) <= 0) {//如果要查找的对象大于或等于当前对象,向右子树查找。
if(this.right == null) {
return null;
}
//递归向右子树查找
return this.right.bstSearch(data);
}
return null;
}
/**
* @Title: inFixOrder
* @Description:中序遍历
* @param:
* @return: void
* @throws
*/
public void inFixOrder() {
//先遍历左子树
if(this.left!=null) {
this.left.inFixOrder();
}
//打印数据
System.out.println(this);
//遍历右子树
if(this.right!=null) {
this.right.inFixOrder();
}
}
/**
* @Title: add
* @Description:添加方法
* 实现:调用 Comparable 接口的 compareTo 方法,比较对象大小
* 1、如果当前对象小于指定对象,返回负整数
* 2、如果当前对象等于指定对象,返回0
* 3、如果当前对象大于指定对象,返回正整数
*
* 如果返回正整数,进左子树
* 如果返回负整数或0,进右子树
* @param: data
* @return: void
* @throws
*/
public void add(Comparable data) {
if(this.data.compareTo(data) > 0) {
if(this.left==null) {
this.left = new Node(data);
}else {
this.left.add(data);
}
}else if(this.data.compareTo(data) <= 0) {
if(this.right == null) {
this.right = new Node(data);
}else {
this.right.add(data);
}
}
}
/**
* @Title: Node
* @Description:
* @param: @param data
* @throws
*/
public Node(Comparable data) {
super();
this.data = data;
}
/**
*
*/
@Override
public String toString() {
return "Node [data=" + data + "]";
}
}
}
测试代码:
/**
* All rights Reserved, Designed By https://www.tulingxueyuan.com/
* @Title: BinarySearchTreeDemo.java
* @Package com.tuling.tree
* @Description:
* @author: 小白
* @Date 2019年12月7日 上午1:18:33
* @version V1.0
* @Copyright:
*/
package com.tuling.tree;
import com.tuling.tree.BinarySearchTree.Node;
/**
* @ClassName BinarySearchTreeDemo
* @Description
* @Author 北京图灵学院
* @Date 2019年12月7日 上午1:18:33
*/
public class BinarySearchTreeDemo {
/**
* @Title: main
* @Description:
* @param: @param args
* @return: void
* @throws
*/
public static void main(String[] args) {
BinarySearchTree bst = new BinarySearchTree();
bst.add(25);
bst.add(43);
bst.add(2);
bst.add(765);
bst.add(23);
bst.add(1);
bst.add(76);
bst.inFixOrder();
System.out.println();
// Node searchNode = bst.bstSearch(76);
// System.out.println(searchNode);
System.out.println("===========删除 25 ===========");
bst.del(2);
bst.inFixOrder();
}
}
4.3. 5.4.平衡查找树¶
4.3.1. 5.4.1.AVL树¶
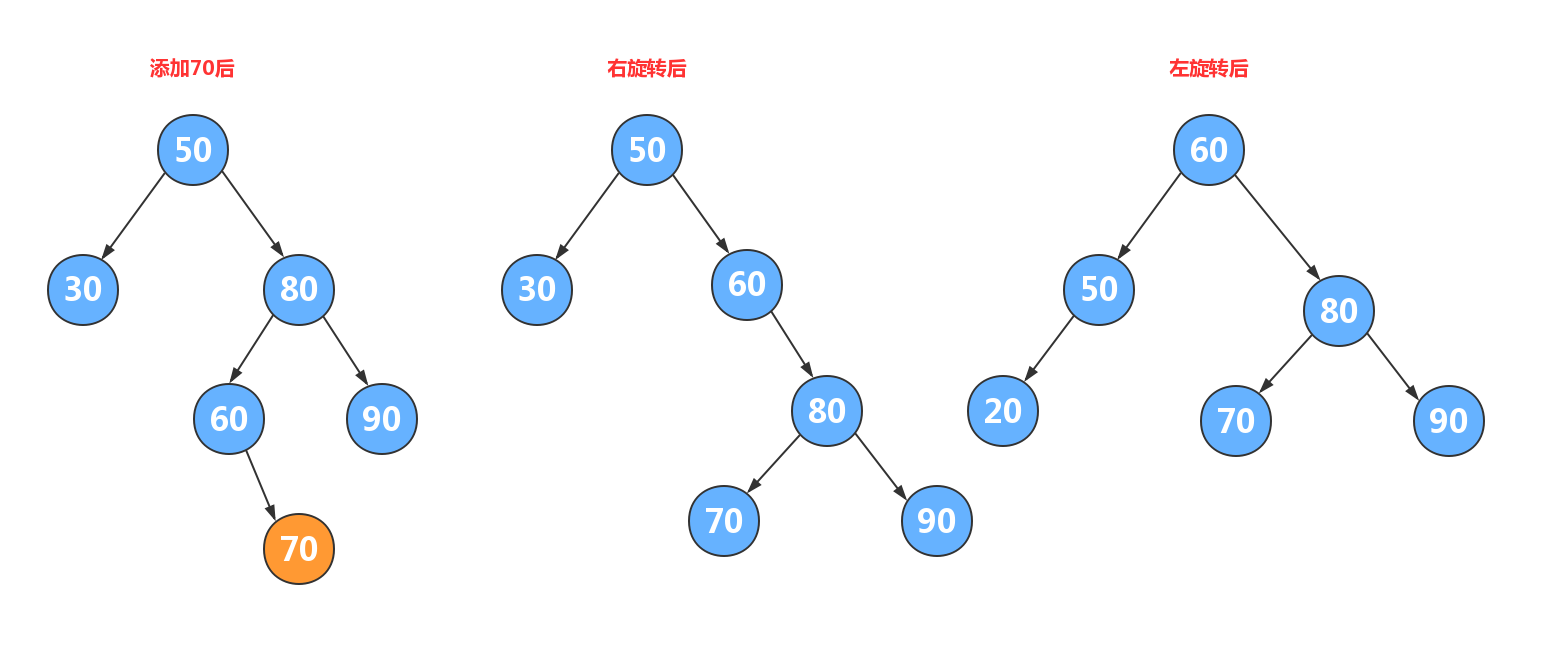
在计算机科学中,AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1,所以它也被称为高度平衡树。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。
4.3.1.1. 5.4.1.1.特点¶
AVL树本质上还是一棵二叉搜索树,它的特点是:
- 本身首先是一棵二叉搜索树。
2. 带有平衡条件:每个结点的左右子树的高度之差的绝对值(平衡因子)最多为1。 也就是说,AVL树,本质上是带了平衡功能的二叉查找树(二叉排序树,二叉搜索树)。
4.3.1.2. 5.4.1.2.单旋转¶
4.3.1.2.1. 5.4.1.2.1.右旋转¶
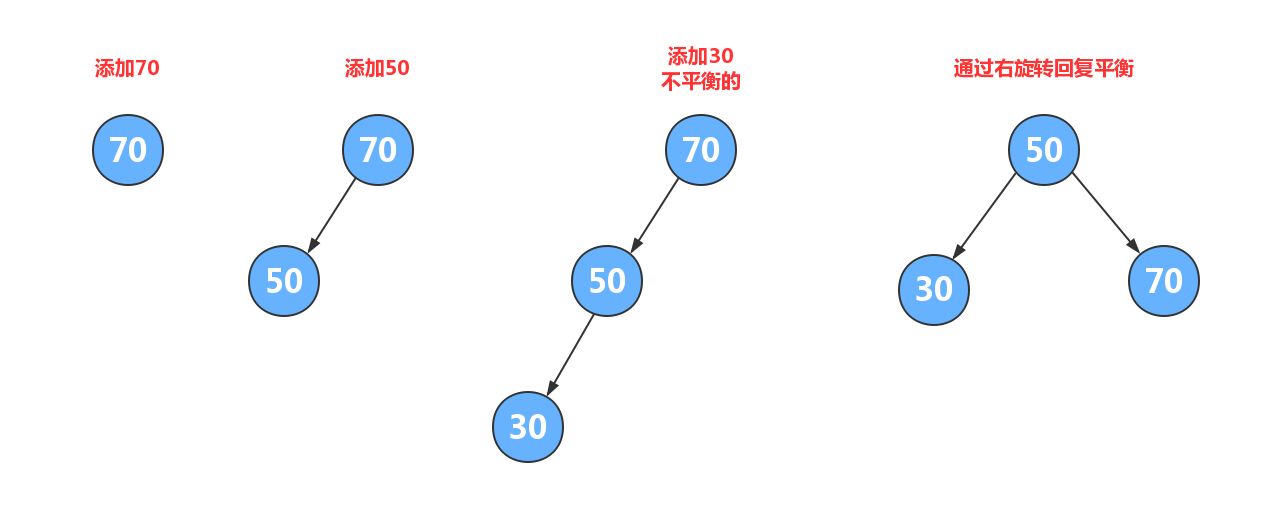
思路分析:
- 回溯找到失去平衡的节点,以该节点为根,创建一个新节点
- 把新节点的右子树设置为当前节点的右子树
- 把新节点的左子树设置为当前节点的左子树的右子树
- 把当前节点的值换为左子节点的值
- 把当前节点的左子树设置为左子树的左子树
- 把当前节点的右子树设置为新节点
代码实现:
/**
* @Title: rotateRight
* @Description:右旋操作
* 1、回溯找到失去平衡的节点,以该节点为根,创建一个新节点
* 2、把新节点的右子树设置为当前节点的右子树
* 3、把新节点的左子树设置为当前节点的左子树的右子树
* 4、把当前节点的值换位左子节点的值
* 5、把当前节点的左子树设置为左子树的左子树
* 6、把当前节点的右子树设置为新节点
* @param:
* @return: void
* @throws
*/
private void rotateRight() {
//1、回溯找到失去平衡的节点,以该节点为根,创建一个新节点
Node tempNode = new Node(data);
//2、把新节点的右子树设置为当前节点的右子树
tempNode.right = right;
//3、把新节点的左子树设置为当前节点的左子树的右子树
tempNode.left = left.right;
//4、把当前节点的值换位左子节点的值
data = left.data;
//5、把当前节点的左子树设置为左子树的左子树
left = left.left;
//6、把当前节点的右子树设置为新节点
right = tempNode;
}
4.3.1.2.2. 5.4.1.2.2.左旋转¶
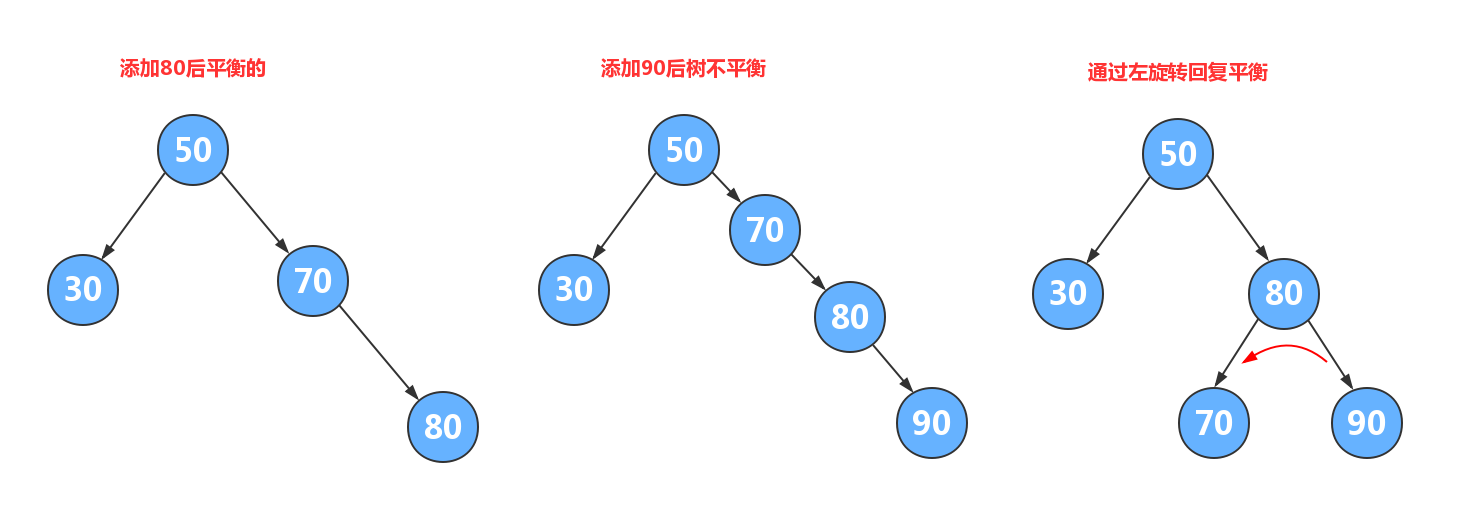
思路分析:
- 回溯找到失去平衡的节点,以该节点为根,创建一个新节点
- 把新节点的左子树设置为当前节点的左子树
- 把新节点的右子树设置为当前节点的右子树的左子树
- 把当前节点的值替换为右子节点的值
- 把当前节点的右子树设置为右子树的右子树
- 把当前节点的左子树设置为新节点
代码实现:
/**
* @Title: rotateLeft
* @Description:左旋操作:
* 1、回溯找到失去平衡的节点,以该节点为根,创建一个新节点
* 2、把新节点的左子树设置为当前节点的左子树
* 3、把新节点的右子树设置为当前节点的右子树的左子树
* 4、把当前节点的值替换为右子节点的值
* 5、把当前节点的右子树设置为右子树的右子树
* 6、把当前节点的左子树设置为新节点
* @param:
* @return: void
* @throws
*/
private void rotateLeft() {
System.out.println("旋转代码中的 data = " + data);
//以根节点为参考,创建新的节点
Node tempNode = new Node(data);
//把新节点的左子树设置为当前节点的左子树
tempNode.setLeft(left);
//把新节点的右子树设置为当前节点的右子树的左子树
tempNode.setRight(right.left);
//把当前节点的值替换为右子树的值
data = right.data;
//把当前节点的右子树设置为当前节点右子树的右子树
right = right.right;
//把当前节点的左子树设置为新节点
left = tempNode;
}
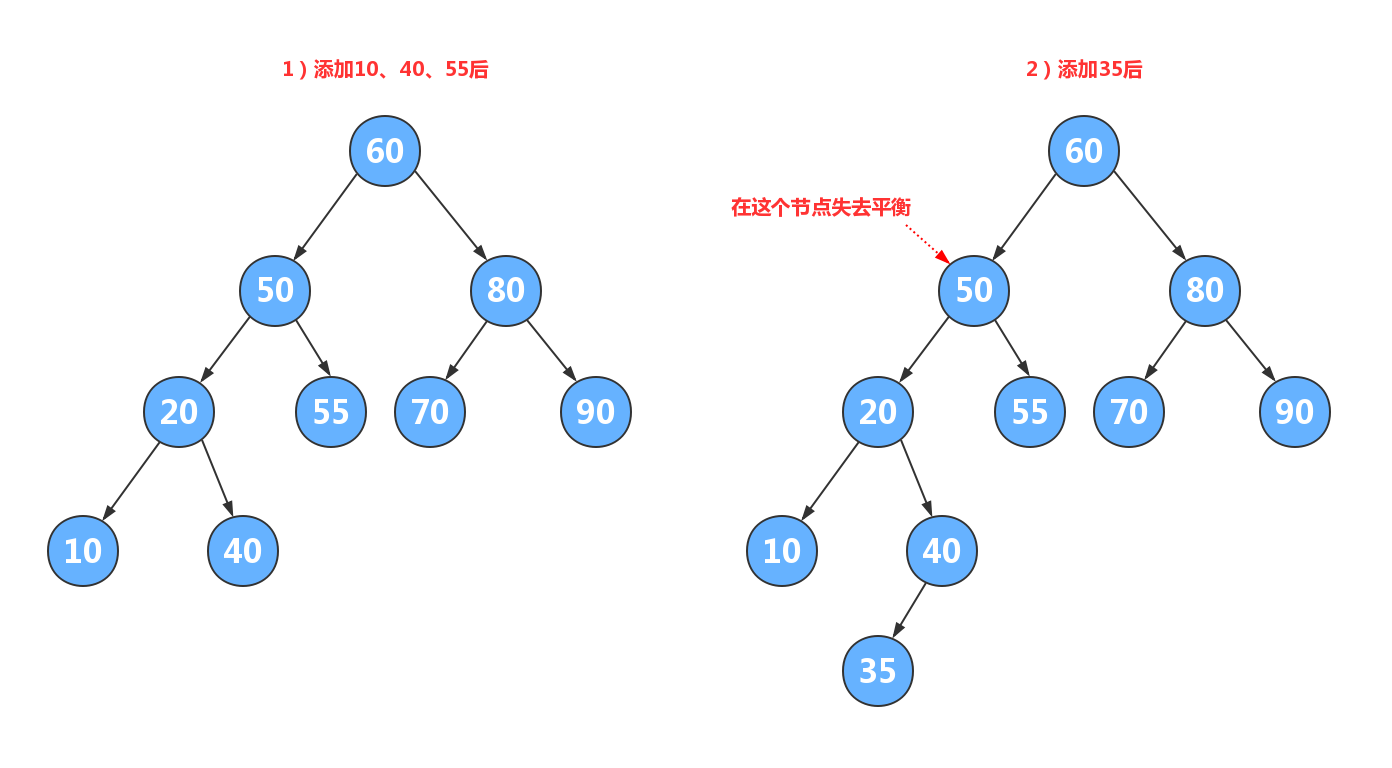
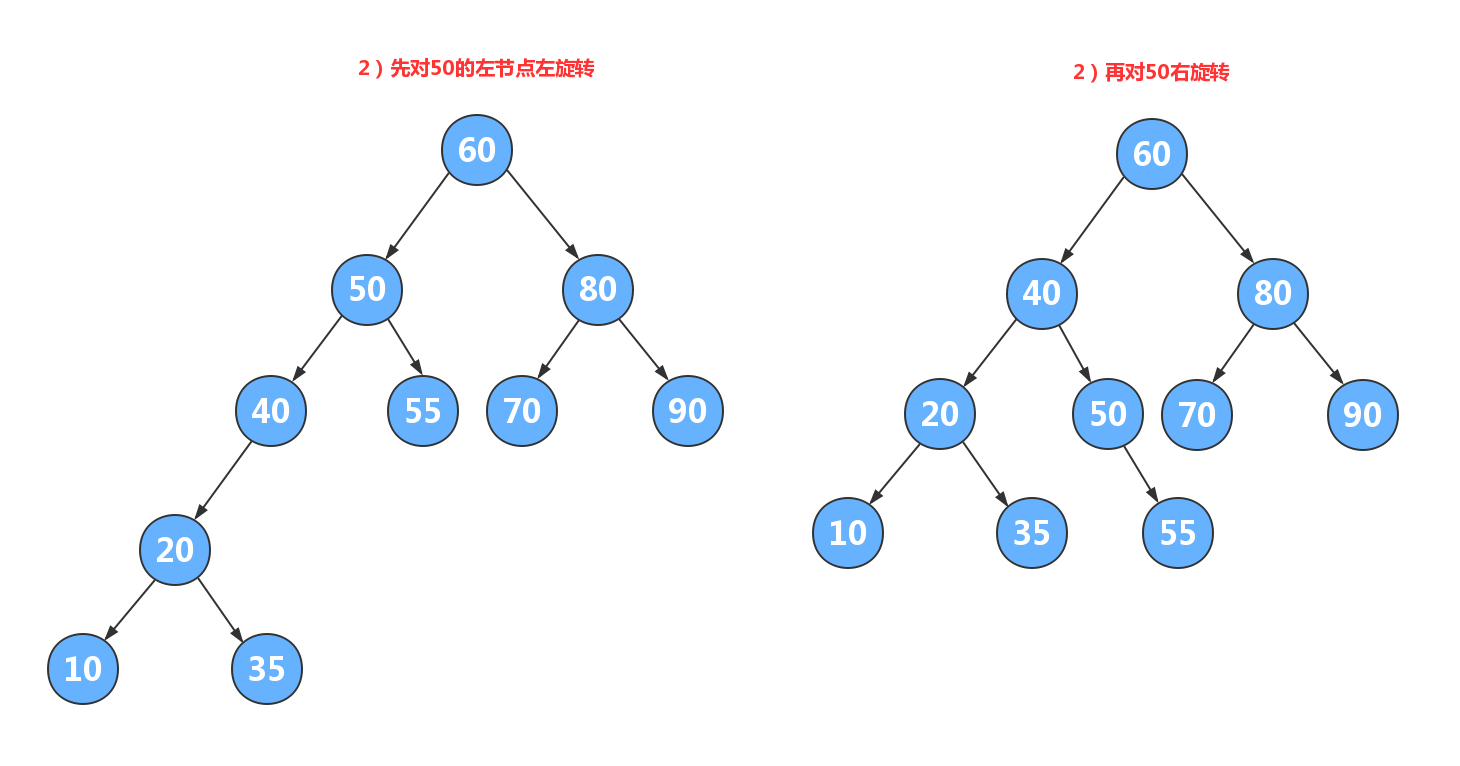
4.3.1.3. 5.4.1.3.双旋转¶
4.3.1.4. 5.4.1.4.实现¶
平衡二叉树实现增加旋转功能完整代码如下:
/**
* All rights Reserved, Designed By https://www.tulingxueyuan.com/
* @Title: AVLTree.java
* @Package com.tuling.tree
* @Description:
* @author: 小白
* @Date 2019年12月8日 下午10:09:37
* @version V1.0
* @Copyright:
*/
package com.tuling.tree;
/**
* @ClassName AVLTree
* @Description
* @Author 北京图灵学院
* @Date 2019年12月8日 下午10:09:37
*/
public class AVLTree {
private Node root;
/**
*
* @Title: add
* @Description:
* @param: @param data
* @return: void
* @throws
*/
public void add(int data) {
System.out.print("当前添加数据:" + data + " ");
if(root == null) {
root = new Node(data);
}else {
root.add(data);
}
}
/**
* @Title: rotateLeft
* @Description:左旋操作
* @param: node
* @return: void
* @throws
*/
private Node rotateLeft(Node nodeN) {
Node nodeC = nodeN.getRight();
nodeN.setRight(nodeC.getLeft());
nodeC.setLeft(nodeN);
return nodeC;
}
public void inFixOrder() {
if(root == null) {
System.out.println("树为空!");
}else {
root.inFixOrder();
}
}
public Node getRoot() {
return root;
}
public void setRoot(Node root) {
this.root = root;
}
class Node{
private Node left,right;
private int data;
/**
* @Title: Node
* @Description:
* @param: @param data
* @throws
*/
public Node(int data) {
this.data = data;
}
/**
* @Title: add
* @Description:
* @param: data
* @return: void
* @throws
*/
public void add(int data) {
if(this.data > data) {
if(this.left == null) {
this.left = new Node(data);
}else {
this.left.add(data);
}
}else if(this.data < data) {
if(this.right == null) {
this.right = new Node(data);
}else {
this.right.add(data);
}
}
//TODO:
//做完添加操作,
if(leftHeight() - rightHeight() > 1) {//如果左子树的高度大于右子树的高度,需要右旋操作。
if(left!=null && this.left.rightHeight()>left.leftHeight()) {
System.out.print("左旋再右旋 -- " + left.data);
//先对当前节点的左孩子进行左旋
left.rotateLeft();
//再进行右旋
rotateRight();
}else {
System.out.print("右旋" + data);
//直接右旋即可
rotateRight();
}
}
if(rightHeight() - leftHeight() > 1) {//如果右子树的高度大于左子树的高度,需要左旋操作
if(right!=null && right.leftHeight()>right.rightHeight()) {
System.out.print("右旋再左旋 -- " + right.data );
//先对象当前节点的右孩子右旋
right.rotateRight();
//再进行左旋操作
rotateLeft();
}else {
System.out.print("左旋 -- " + data);
//直接左旋节课
rotateLeft();
}
}
}
/**
* @Title: rotateRight
* @Description:右旋操作
* 1、回溯找到失去平衡的节点,以该节点为根,创建一个新节点
* 2、把新节点的右子树设置为当前节点的右子树
* 3、把新节点的左子树设置为当前节点的左子树的右子树
* 4、把当前节点的值换位左子节点的值
* 5、把当前节点的左子树设置为左子树的左子树
* 6、把当前节点的右子树设置为新节点
* @param:
* @return: void
* @throws
*/
private void rotateRight() {
//1、回溯找到失去平衡的节点,以该节点为根,创建一个新节点
Node tempNode = new Node(data);
//2、把新节点的右子树设置为当前节点的右子树
tempNode.right = right;
//3、把新节点的左子树设置为当前节点的左子树的右子树
tempNode.left = left.right;
//4、把当前节点的值换位左子节点的值
data = left.data;
//5、把当前节点的左子树设置为左子树的左子树
left = left.left;
//6、把当前节点的右子树设置为新节点
right = tempNode;
}
/**
* @Title: rotateLeft
* @Description:左旋操作:
* 1、回溯找到失去平衡的节点,以该节点为根,创建一个新节点
* 2、把新节点的左子树设置为当前节点的左子树
* 3、把新节点的右子树设置为当前节点的右子树的左子树
* 4、把当前节点的值替换为右子节点的值
* 5、把当前节点的右子树设置为右子树的右子树
* 6、把当前节点的左子树设置为新节点
* @param:
* @return: void
* @throws
*/
private void rotateLeft() {
System.out.println("旋转代码中的 data = " + data);
//以根节点为参考,创建新的节点
Node tempNode = new Node(data);
//把新节点的左子树设置为当前节点的左子树
tempNode.setLeft(left);
//把新节点的右子树设置为当前节点的右子树的左子树
tempNode.setRight(right.left);
//把当前节点的值替换为右子树的值
data = right.data;
//把当前节点的右子树设置为当前节点右子树的右子树
right = right.right;
//把当前节点的左子树设置为新节点
left = tempNode;
}
/**
* @Title: rightHeight
* @Description:
* @param: @return
* @return: int
* @throws
*/
private int rightHeight() {
if(right == null) {
return 0;
}
return height(right);
}
/**
* @Title: height
* @Description:
* @param:
* @return: int
* @throws
*/
private int height(Node node) {
if(node == null) return 0;
return 1+Math.max(height(node.left), height(node.right));
}
/**
* @Title: leftHeight
* @Description:
* @param: @return
* @return: int
* @throws
*/
private int leftHeight() {
if(left == null)return 0;
return height(left);
}
/**
* @Title: inFixOrder
* @Description:
* @param:
* @return: void
* @throws
*/
public void inFixOrder() {
if(this.left!=null) {
this.left.inFixOrder();
}
System.out.println(this.data);
if(this.right!=null) {
this.right.inFixOrder();
}
}
public Node getLeft() {
return left;
}
public void setLeft(Node left) {
this.left = left;
}
public Node getRight() {
return right;
}
public void setRight(Node right) {
this.right = right;
}
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
}
}